Recently discovered issues with the IPE160 beam and alternative solutions

For the given types of load exerted on the standard IPE160 beam the deflection, BMmax and SFmax were obtained to indicate worst case conditions that the given material (steel grade) would need to withstand:



The next stage was to calculate the maxBM and maxSF for the given structural steel. If these values are found to be higher than the calculated maxBM and maxSF under load then the beam will not fail. The following formulas were used:

M = Z *("fy") where Z = I/y (for the moment)
Where “fy” = steel grade

V= "dw"*"tw"*("fy"/(3)^(1/2)) (for the shear force)

Formulas and following information courtesy of:
The Corus interactive “blue book” to BS 5950-1
BS 4: part1:1993
BS 5950-12000 part 1
Elements of Strength of Materials, International Student Edition, by S Timoshenko

To calculate the maxBM:

M = Z ("fy")
Note:
Z = I/y and y= D/2

“fy”= common steel grade S250= 250 N/mm^2
( i.e for the given 5mm thickness the required design strength is 250N/mm^2)



I=8.34E-06 m^4 or 8.34E+06 mm^4

D/2 =160mm/2= 80mm

Therefore Z =I/y = (8.34E+06 mm^4/80mm)
Z =104250mm^3

M=Z* “fy”

M=104250mm^3 * 250 N/mm^2
M=26.06E+06 Nmm
M=26.06 kNm

In order to obtain the maxBM a factor of safety rm=1.05 and rf=1.1 provided in the Corus interactive “blue book” to BS 5950-1 need to be included:

Md =M/rm*rf
Md =26.06/1.05*1.1
Md =22.5 kNm

This is the maxBM that this steel grade could withstand.

For max shear force that the beam would need to withstand:
V ="dw"*"tw"*("fy"/(3)^(1/2))
V= 5* 145.2*(250/(3)^(1/2))
V=104789N or 104.789kN

However another factor mentioned in the Corus interactive ” blue book” is to have a safety capacity related to Buckling (some tables are given ):



Therefore a major issue with this beam is the maxBM allowable due to consideration of safety factors and buckling.
Further research also found IPE160 to be a castellated beam type which further impacts on strength but also increases the general cost of the material.

To obtain a more suitable beam a different standard will be used and a steel grade S355:



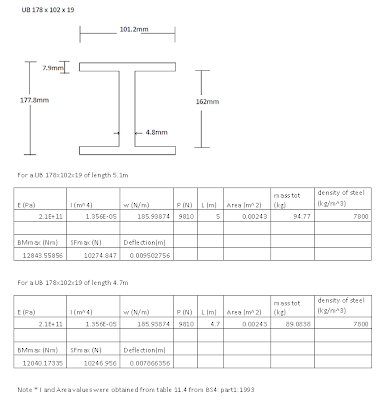
The next stage was to calculate the maxBM and maxSF for the given structural steel. If these values are found to be higher than the calculated maxBM and maxSF under load then the beam will not fail.

I=1.356E-05 m^4 or 1.356E+07 mm^4

D/2 =177.8mm/2= 88.9mm
Therefore Z =I/y = (1.356E+07 mm^4/88.9mm)
Z=152530.9336mm^3

M=Z* “fy”

M=152530.9336mm^3 * 355 N/mm^2
M=54.148E+06 Nmm
M=54.148 kNm

In order to obtain the maxBM a factor of safety rm=1.05 and rf=1.1 provided in the “blue book” to BS 5950-1 need to be included:

Md =M/rm*rf
Md =54.148/1.05*1.1
Md =46.881 kNm

This is the maxBM that this steel grade could withstand.

For max shear force that the beam would need to withstand:
V ="dw"*"tw"*("fy"/(3)^(1/2))
V= 4.8* 146.8*(355/(3)^(1/2))
V=144422.553N or 144.423kN

However another factor mentioned in the Corus interactive "blue book” is to have a safety capacity related to Buckling (the following value is from table “4.1.3. bending. Advance UKB. Moment capacity and buckling resistance moment for Advance 355”):

Md =17kNm



This beam clearly passes the basic required criteria and so long as these loading conditions are maintained it should not fail for the duration of the service for the disaster relief (if a 4.7m beam were to be used the buckling resistance moment would be higher than 17kNm).

The following are the lists of tables used from the BS standards :